Recursie

Om recursie te kunnen begrijpen moet je eerst recursie kunnen begrijpen.

– student, anoniem

Of: het antwoord op het probleem is het antwoord op het probleem (is het antwoord op het probleem)

Zet je schrap want dit onderwerp gaat voor hoofpijn én verassende inzichten zorgen, kies je favoriet…

Een oplossing die zichzelf herhaalt

def numis(s):
    """Tel het aantal i's in s
    input s: een string
    """
    ...

Stel je een functie voor die het aantal i’s in een string telt en dit als waarde teruggeeft. Dit is een lastig probleem, laten we proberen het eerst uit te schrijven zonder direct in Python te denken. Het resultaat van de functie zou het volgende moeten zijn:

Totaal aantal i’s in "i💙aliens"?

Aliens zijn om van te houden, toch?!? Laat dit de string zijn die we willen gaan onderzoeken en je weet dat een string een opeenvolging van karakters is. We zullen karakter voor karakter moeten controleren (testen) of het gelijk is aan het karakter “i” (en ja, emoji zijn ook karakters :heart:). Karakter voor karakter betekent dat een eerste stap om dit probleem op te lossen de volgende zal zijn:

Aantal i’s in "i" + Aantal i’s in "💙aliens"

We nemen het eerst karakter, tellen het aantal i’s (dit kan voor een enkel karakter 0 of 1 zijn) en tellen daar het aantal i’s in het restant van de string bij op. We herhalen deze handeling voor het eerste karakter van het restant, en tellen daar natuurlijk het resultaat van het eerste karakter bij op:

Aantal i’s in "i" + Aantal i’s in "💙" + Aantal i’s in "aliens"

Et cetera. Je zal hier een patroon zien, het probleem en oplossing herhaalt zich steeds: na het eerste karakter moeten we hetzelfde “recept” steeds weer herhalen voor het restant van de string.

Terzijde, weet je nog dat je het eerste karakter en het restant van een string kan lezen met s[0] en s[1:]?

Paradigmas

Verschillende manieren om dit probleem dit op te lossen:

sequentieeel (iteratief)

zelfgelijkend (recursief)

Het numis(s) probleem valt op meer dan één manier op te lossen en we komen daarmee aan bij het bestaan van verschillende programmeerparadigmas, dat wil zeggen technieken en benaderingen voor het oplossen van een probleem. We gaan eerst recursie verkennen, een iteratieve benadering komt later.

Als je al eerder (meer of minder) hebt geprogrammeerd zal je iteratieve constructies wellicht kennen als lussen (bijvoobeeld “while” of “for each” lussen), deze benadering gaan we nu dus niet gebruiken!

Sequentieel denken

faculteit

wiskunde: \(5! = 120\)

informatica: fac(5) = 5 * 4 * 3 * 2 * 1

Laten we het geheugen even opfrissen wat de faculteit van een getal ook alweer is. Stel je 42 aliens voor en je zou willen weten op hoeveel manieren je deze aliens op een rij kan zetten. Je weet misschien het antwoord, dit is 42 x 41 x 41 … 3 x 2 x 1, of ook wel bekend als de 42 faculteit en (wiskundig) geschreven als \(42!\). Sequentieel denken en daarmee dit probleem oplossen (uitschrijven) als 5 * 4 * 3 * 2 * 1 is heel natuurlijk voor mensen, zo hebben we het als oplossing geleerd!

fac(N) = N * (N-1) * ... * 3 * 2 * 1

Maar zou je fac(5) als een meer algemene versie van zichzelf kunnen schrijven? Dat kan, laten we daar een begin mee maken en je zal zien dat een zichzelf herhalend (terugkerend?) patroon gaat ontstaan, net als bij het aantal i’s in "i💙aliens"…

Recursief denken

faculteit

wiskunde: \(5! = 120\)

informatica: fac(5) = 5 * 4 * 3 * 2 * 1

fac(5) = 5 * fac(4)

fac(N) = N * fac(N - 1)

Dit is correct…

def fac(N):
    return N * fac(N - 1)

maar is niet aan te raden…

Je kan de funcie fac(N) met de meest algemene vorm (oplossing) nu invulllen. De functie roept zichelf aan met steeds N-1, dit is het patroon dat we hebben kunnen ontdekken. Maar dit is niet volledig correct zoals je misschien zelf al kan zien?

Loop in gedachten eens na wat er gebeurt als je 1 hebt bereikt in deze functie, het zal vrolijk fac(N-1) blijven aanroepen! Dit zal dus doorgaan in een “oneindige recursie” want we hebben nog geen rekening gehouden met de “base case”, het geval waar geen recursieve aanroep meer mogelijk is.

Is het correct?

def fac(N):
    return N * fac(N - 1)

Een base case ontbreekt, de noodstop!

Er is een duidelijk moment dat we de recursie moeten beëindigen, het moment dat geen recursieve aanroep meer mogelijk is. Dit is het moment dat de base case is bereikt (de “noodzakelijk” stop). N-1 gaat uiteindelijk naar negatieve getallen, zou de waarde 0 in dit geval de noodzakelijke stop (de base case) kunnen zijn?

Recursief denken

def fac(N):
    if N == 0:  # base case 
        return 1
    else:       # recursive case
        return N * fac(N - 1)

Je kan testen op de base case, in het geval van een faculteit is dit bereikt als N gelijk is aan 0. Maar als je naar de laatste regel kijkt (N * fac(N-1)), hoe kan iets (N) vermenigvudigd worden met iets dat nog niet is uitgevoerd (fac(N-1))?

Recursief handelen

def fac(N):
    if N == 0:  # base case
        return 1
    else:       # recursive case
        rest = fac(N - 1)
        return N * rest

Deze uitwerking is meer in de buurt van wat achter schermen gebeurt. In het geval N * fac(N - 1) wordt door de computer de recursieve aanroep (fac(N - 1)) eerst aangeroepen om vervolgens daar N mee te vermenigvuldigen. Je kan dit goed vergelijken met het eerst zetten van een variabele (rest in dit geval) die later wordt gebruikt om het antwoord te berekenen (N * rest).

Stapelen

Recursief stapelen!

Recursieve aanroepen van functies worden gestapeld, zoals je al eerder hebt gezien! Van onder naar boven worden de frames van de stack gehaald en resultaten naar het bovenliggend frame doorgegeven.

De aanroepen zijn gestapeld in 5 frames (we tellen het globale frame even niet mee). Elk frame wacht nu op het resultaat van het onderliggende frame.

Bij het laatste frame (N = 0) wordt de base case bereikt en het geeft 1 als returnwaarde terug aan het bovenliggende frame.

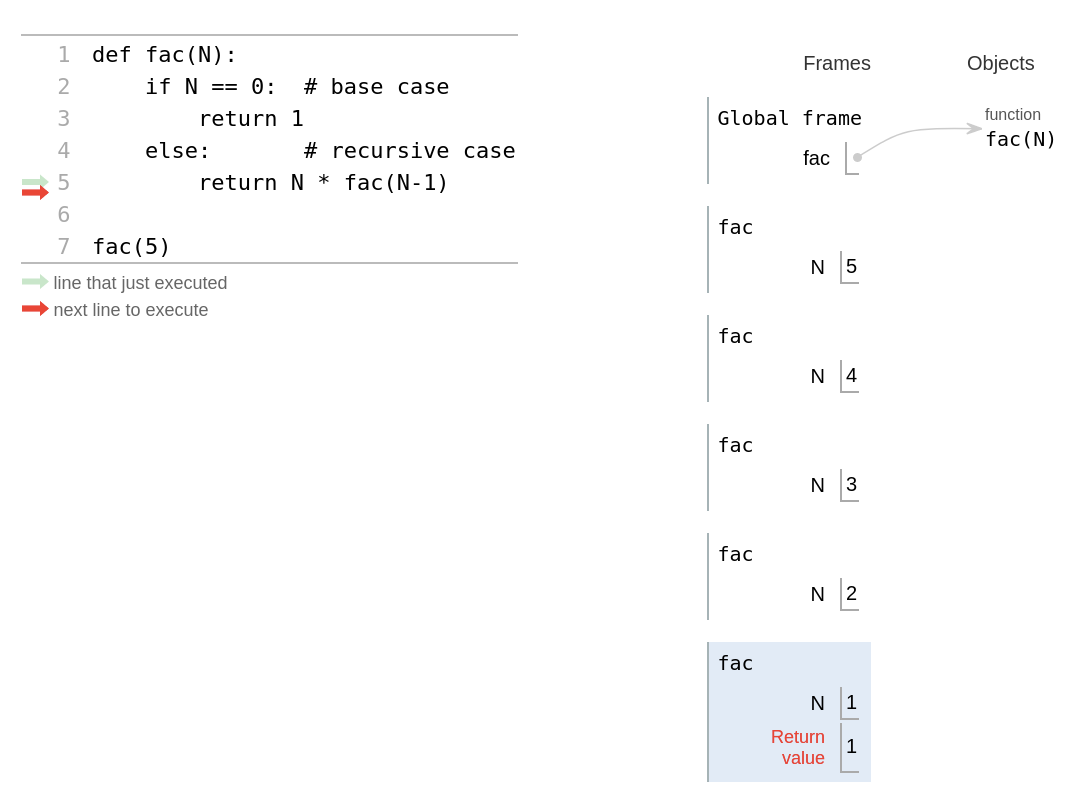
En zo geeft het volgende frame steeds de returnwaarde terug aan het bovenliggende frame!

Tot de uiteindelijke oplossing is bereikt, fac(5) is gelijk aan 120.

De uitdaging

De uitdaging van het oplossen van recursief handelen is om zowel het geheel als de zelfgelijkende delen te zien!

Je komt trouwens veel voorbeelden van recursie in de natuur tegen, later zie je meer voorbeelden!

Recursie

Recursie als een paradigma voor het oplossen van problemen

• een base case, en

• een zelfgelijkend ontwerp

Recursie is een belangrijk patroon, of paradigma voor het oplossen van problemen. Bedenk dat er altijd een base case en een zelfgelijkend ontwerp aanwezig moet zijn. Zelfgelijkend is in dit geval dat we dezelfde oplossing steeds kunnen toepassen op een deel van het probleem.

Recursief ontwerp

Faculteit: fac(x)

fac(5):

• fac(5) is de waarde van 5*4*3*2*1 en is gelijk aan

• de waarde 5 * (4*3*2*1), wat gelijk is aan 5 * fac(4)

De base case:

• fac(0) moet 1 teruggeven

Dit is het voorbeeld dat we net in detail hebben bekeken, tot en met hoe het stapelt…

def fac(x):
    """faculteit, recursief!    
    """
    if x == 0:  # base case
        return 1
    else:       # recursive case
        return x * fac(x-1)

assert fac(0) == 1    # test de base case
assert fac(5) == 120  # test de oplossing  

We herhalen de code nog een keer: met tests (in dit geval assert statements) kan je bepalen of je te maken hebt met de base case, of dat een recursieve aanroep moet worden gedaan. En bedenk nogmaals, zonder een base case zal je in een oneindige recursie terecht komen!

Terzijde, Python zal jou tegen een eindeloze recursie beschermen omdat het standaard een maximale diepte (het aantal frames) heeft geconfigureerd voor de recursieve aanroep van een functie (3000 is de limiet). Een stack overflow fout zal je dus niet snel zien en de limiet kan je aanpassen, als het nodig is!

Optelling: plusone(n)

plusone(5):

• plusone(5) is de waarde van 1+1+1+1+1 en is gelijk aan

• de waarde 1 + (...), wat gelijk is aan 1 + plusone(...)

De base case:

• plusone(0) moet … teruggeven

Een ander voorbeeld. plusone(n) telt n door 1-en op te tellen. Als n gelijk is aan 5 dan worden 5 1-en bij elkaar opgeteld. Hoe kan je dit recursief oplossen? Denk altijd aan eerst aan de base case, in welk geval is is geen recursie meer mogelijk? Wat moet in dit geval voor de ... moeten worden ingevuld voor de base en recursieve case?

def plusone(n):
    """Geeft n terug door 1-en op te tellen!
    """
    if n == 0:  # base case
        return ...
    else:       # recursive case
        return ...

De ... zie je hier in de code terug. Wat moet voor de base- en recursieve case worden ingevuld? Denk hier terug aan aan fac(x), hetzelfde patroon zal je hier moeten volgen!

Oplossing

def plusone(n):
    """Geeft n terug door 1-en op te tellen!
    """
    if n == 0:  # base case
        return 0
    else:       # recursive case
        return 1 + plusone(n-1)

assert plusone(0) == 0  # test de base case
assert plusone(5) == 5  # test de oplossing

De recursieve case moet hier voor elke n-1 worden herhaald, zoals je ook bij fac(x) hebt gezien.

Machtverheffing: pow(b, p)

pow(2, 5):

• pow(2, 5) is de waarde van 2*2*2*2*2 en is gelijk aan

• 2 * (...), wat gelijk is aan 2 * pow(..., ...)

De base case:

pow(2, 0) moet … teruggeven

def pow(b, p):
    """b**p, recursief!
    """
    if p == 0:  # base case
        return ...
    else:       # recursive case
        return ...

Ook hier kan je een base- en recursive case ontdekken. Laten we het uitschrijven:

Oplossing

def pow(b, p):
    """b**p, recursief!
    """
    if p == 0:  # base case
        return 1.0
    elif p < 0: # tweede base case? of een recursive case?
        ...
    else:       # recursive case
        return b * pow(b, p-1)

assert pow(2, 0) == 1.0   # test de base case
assert pow(2, 5) == 32.0  # test de oplossing

Er is hier meer uitgeschreven dan je zou verwachten! Want, wat moet je doen in het geval dat de exponent p een negatief getal is? Is dit een base- of recursive case?!?

Een machtsverheffing met grondtal \(b\) en negatieve exponent \(p\)

\[ {b^{⁻p}} \]

kan herschreven kan worden als

\[ \frac{1}{b^p} \]

Misschien moet je hier wat wiskundige kennis afstoffen! We gaan niet verder op de achtergrond in en nemen dit ter kennisgeving aan… Het roept wel een andere vraag op, namelijk hoe we Python een negatief getal kunnen laten omzetten naar de positieve waarde? Of, meer in het algemeen, de omkering van een willekeuringe waarde (met andere woorden, de logische negatie van een waarde)?

p = -5

-p

5

Dit probleem komt zo vaak voor dat het ook in syntax is geïmplementeerd! Probeer in dit geval ook eens als p = 5. We kunnen dit nu gaan toepassen op de recursieve case in het geval exponent p een negatieve waarde heeft.

Oplossing

def pow(b, p):
    """b**p, recursief!
    """
    if p == 0:   # base case
        return 1.0
    elif p < 0:  # recursive case (p negatief)
        return 1.0 / pow(b, -p)
    else:        # resursive case (p positief)
        return b * pow(b, p-1)

assert pow(2, 0) == 1.0       # test de base case
assert pow(2, 5) == 32.0      # test de oplossing
assert pow(2, -5) == 0.03125  # test de oplossing

Voordelen van recursie

Het kan zelfstandig in één keer een willekeurige diepte ingaan

De functie heeft aan zichzelf genoeg en met één aanroep (van ons) lost het zichzelf tot elke willekeurige diepte op!

Romanesco is een groente met prachtige recursieve patronen.

Maar is recursie ook bij ons te vinden?

Misschien, maar gelukkig heeft ons lichaam wél de base case goed gedefinieerd!

Python is in

Bevind een element zich in een sequentie (een list, een string, …)?

Dit probleem zal je vaak gaan tegenkomen: bijvoorbeeld bij de vraag of “i” een klinker is? Klinkers zijn de karakters a, e, i, o en u. Dit kan je als een sequentie schrijven, bijvoorbeeld als string "aeiou" of als list ["a", "e", "i", "o", "u"]. Python kent de in operator om te testen of een element zich in een sequentie bevindt, bijvoorbeeld "i" in "aeiou". Een paar voorbeelden:

is in string

"i" in "team"

False

"i" in "alien"

True

3*"i" in "aliiien"

True

is in list

42 in [41, 42, 42]

True

42 in [[42], "42"]

False

Kan je uitleggen waarom de laatste False teruggeeft?

Meer voorbeelden

Aantal klinkers: vwl(s)

vwl("zaaiuien")

• vwl("zaaiuien") is het aantal klinkers in “zaaiuien” en is gelijk aan

• het aantal klinkers in “z” + het aantal klinkers in vwl(...)

De base case:

vwl("") moet … teruggeven

def vwl(s):
    """Tel het aantal klinkers in s
    """
    if s == "":
        ...
    elif ...:
        return ...
    else:
        return ...

Oplossing

def vwl(s):
    """Tel het aantal klinkers in s
    """
    if s == "":
        return 0
    elif s[0] in "aeiou":
        return 1 + vwl(s[1:])
    else:
        return vwl(s[1:])

vwl("zaaiuien")

6

Alleen klinkers: keepvwl(s)

keepvwl("pluto")

• keepvwl("pluto") is “pluto” zonder medeklinkers en is gelijk aan

• de klinkers in “p” + de klinkers in keepvwl(...)

De base case:

keepvwl("") moet … teruggeven

def keepvwl(s):
    """Geef ALLEEN de klinkers in s terug
    """
    if s == "":
        return ...
    elif ...:
        return ...
    else:
        return ...

Oplossing

def keepvwl(s):
    """Geef ALLEEN de klinkers in s terug
    """
    if s == "":
        return ""
    elif s[0] in "aeiou":
        return s[0] + keepvwl(s[1:])
    else:
        return keepvwl(s[1:])

keepvwl("pluto")

'uo'

Het hoogste getal: max(L)

max([7, 5, 9, 2])

• max([7, 5, 9, 2]) geeft het hoogste getal terug en is

• 7 of het hoogste getal in max(...)

De base case:

als len(L) == 1 dan moet max(L) … teruggeven

def max(L):
    """Geef de grootste waarde van L terug
    """
    if len(L) == 1:
        return ...
    
    M = ...  # De max van het RESTANT van L
    
    if ...:
        return ...
    else:
        return ...

Oplossing

def max(L):
    """Geef de grootste waarde van L terug
    """
    if len(L) == 1:
        return L[0]
    
    M = max(L[1:])  # De max van de REST van L
    
    print("M is", M, "en L[0] is", L[0])  # test, print M en L[0]
    
    if L[0] > M:
        return L[0]
    else:
        return M

max([7, 5, 9, 2])

M is 2 en L[0] is 9
M is 9 en L[0] is 5
M is 9 en L[0] is 7

9

Je ziet dat we een print statement hebben toegevoegd nét na het moment dat de waarde van M bekend is. Het eerste print statement zegt ons dat M gelijk is aan 2, dit is het laatste element in de lijst L. Waarom het laatste element als eerste geprint?

Als we steeds de functie max met het restant van L aanroepen dan zal het laatste restant 1 element bevatten (de waarde 2) en dit is de base case! L[0] is in dit geval 9 en dit is het één na laatste element. De lijst wordt van achteren naar voren doorlopen en je ziet hier de stack in actie!

Spring eerst, kijk later

max(L) is een goed voorbeeld van een spring eerst (recursie) en kijk later (test) strategie!

Denk ook hier weer aan de stack, werk door tot en met de base case, in dit geval door eerst de recursieve aanroep te doen (M = max(L[1:])) voordat je gaat controleren (if L[0] > M etc.).

Dichtst bij 0: zeroest(L)

zeroest([-7, 5, 9, 2])

• zeroest([-7, 5, 9, 2]) geeft getal het dichtst bij 0 terug en is

• -7 of het getal het dichtst bij 0 in zeroest(...)

De base case:

als len(L) == 1 dan moet zeroest(L) … teruggeven

def zeroest(L):
    """Geef het getal in L het dichtst bij 0 terug
    """
    if len(L) == 1:
        return ...
    
    Z = ...  #  Getal dichtst bij 0 van de REST van L
    
    if ...:
        return ...
    else:
        return ...

Oplossing

def zeroest(L):
    """Return L's element nearest to 0
    """
    if len(L) == 1:
        return L[0]
    
    Z = zeroest(L[1:])  # The zeroest of the REST of L
    
    if abs(L[0]) < abs(Z):
        return L[0]
    else:
        return Z

zeroest([-7, 5, 9, 2])

2